KMP算法

前言

KMP是一种用于字符串匹配的算法，就是从一个字符串中寻找另一个子串

老实说，第一次接触这个算法的时候看的那是一头雾水，代码相当简洁，但是众所周知，代码越简单就代表越难理解: (

同时KMP算法的应用是非常广泛的，AC自动机就是利用KMP算法实现的，浏览器中上亿个关键字也是通过这种方式检索的，有关字符串匹配的相关问题都和KMP脱不了干系

接下来让我们一起来了解一下这个精妙的算法

暴力匹配

当遇到字符串匹配问题时，第一反应是使用蛮力法来一个一个比对，一旦匹配失败就调回主串的下一个字符重新匹配，问题很明显，只要数据量过大，运行就会很慢

考虑到最坏的情况，蛮力法的时间复杂度为N（n*m）

KMP王朝

因为暴力匹配实在是太慢了，于是3位大佬Knuth，Morris，Pratt（即KMP）发表了一个新的算法，把时间复杂度优化到了N（n+m），变成了线性时间复杂度，也就是说在一次遍历之中就能完成字符串的匹配

KMP的本质是利用已知的信息来减少重复的运算，在暴力匹配中，只要遇到不匹配的字符就会将整个数组后移，然后重新匹配，但是我们已经知道之前遍历过的字符，那么我们怎么利用这些信息来避免暴力匹配的“回退”步骤呢

换句话来说，就是让指针不后退，而让它永远向前移动

这就是KMP的其中一个精妙之处了，KMP定义了一个叫做Next数组的概念，先不管Next数组怎么生成的，我们先来详细讲解一下Next数组的用处

Next数组的功能与用途

下面是一个很常见的字符数组，当运行到红色处时发现匹配错误

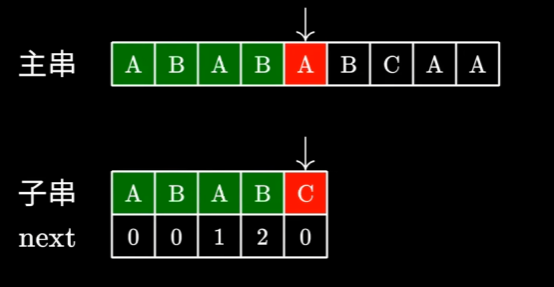
当遇到匹配错误时，就会去看最后一个匹配的字符所对应的Next数值

如图所示，这里使用的next数值就是2，那么我们就直接跳过前面俩个字符，也就是说next数组代表着要跳过的字符个数

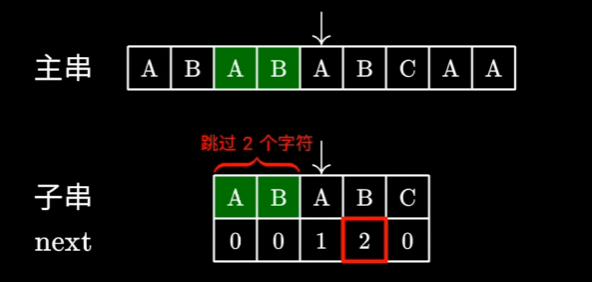
这样我们就实现了不再回退指针（重点），只需要一次遍历就能完成匹配，效率就会高得多

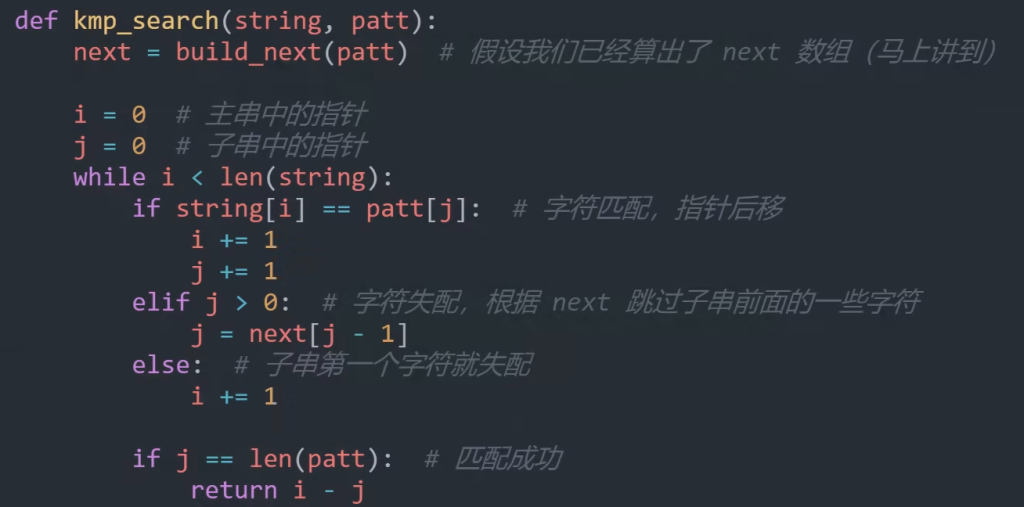
Python代码实现

这里需要指出一个概念，PM表与Next表，其实上图的这种严格意义上来说是PM表（Partial Match部分匹配表），Next表指的是当匹配失败时，模式串指针应该回退的位置，而PM表指的是最长相同前后缀长度（后面会讲到），一定一定不要搞混了，再次重申，本文的Next数组不是真正的Next数组！！！而是PM表！！！

Next的第一种写法就是整个数组向后平移一位，再在第一位补-1或者不补

第二种写法是给第一种都加1，也就是前两位一直是0

经过这样的改写后才是真正意义上的Next数组，可自行百度

Next数组的原理

这个才是KMP的重中之重，想一想，为什么能跳过2个字符呢，就不会漏掉字符吗

其实在推导下这样是不会出现漏掉字符的问题的，注意看，主串的后缀集合与子串的前缀集合是一样的，这句话也等同于为子串的前缀集合与它本身后缀集合的交集（重点），读者自行思考一下

我们再次来看看这张图片，图中跳过了2个字符，为啥一定是2个呢，因为成功匹配的最后这俩AB，和跳过的这俩AB是完全一样的，也就是说，这4个字符，它们有着相同的最长前后缀AB，而这个前后缀的长度刚好为2

可知，我们使用的Next数组就是用来找子串的最长相同前后缀的，一定一定是最长的前后缀，且不含它本身

Next数组的构建

现在我们知道了Next数组的原理，那么算法该怎么写呢

当然，可以for暴力求解，就是效率低了点（乐）

我们可以用递推的方式来求解，利用已有的数据来避免重复运算

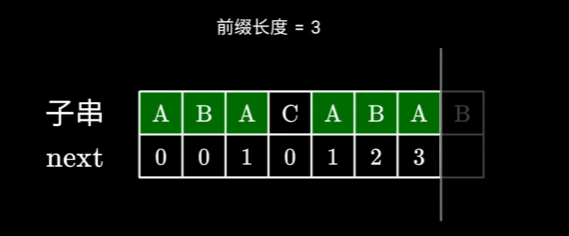
这里分为俩种情况，第一种情况就是下一个字符能构成一个更长的相同前后缀

如图，当运行到第5个字符时，我们已经发现了最长前后缀为AB，即Next为2，在第6个字符时我们发现能构成一个更长的前后缀了，即ABA，那么长度就为2+1，Next就为3

第二种情况就是下一个字符无法构成更长的前后缀，如图ABAC与ABAB无法匹配，那么怎么办呢，难不成又暴力匹配，从0开始数吗？

我们可以发现，子串前后这俩部分完全相同（ABA与ABA），右边这部分的后缀等于左边这部分的后缀，刚好，左边部分的Next已经算过了，直接查表就能发现Next为1，然后又开始匹配，发现AB与AB又能构成相同前后缀了，Next = 1 + 1，即Next为2

Python代码实现

另一种解释

在网上查阅资料时发现了一个很有意思的说法，是通过信号波的角度来解释KMP的概念

https://zhuanlan.zhihu.com/p/661673949

读者可以自行阅读学习

本文章采用 CC BY 4.0 协议进行许可